How to Learn Algebra

Algebra represents the first big intellectual leap in your math class, so it’s no wonder it’s often intimidating for new students. But there are really only two things you need to know in basic algebra: the concept of variables, and how you can manipulate them. The easiest way to learn algebra is how your teachers will teach you. one small step at a time, which you'll repeat over and over again to help sink in each concept to prepare you for the next one.

Quick Summary

Learning algebra begins with mastering basic math operations like addition, subtraction, multiplication, and division. It is important to understand the variables, applications, and transformations of the equations. Use it to solve equations, use pictures, and take trivia tests. Be prepared for non-whole number answers and consider developing skills through factoring. Ask professors or educational resources for help with difficult topics. With dedication and practice, algebra becomes manageable and useful.

1. Learning Basic Algebra Rules

Review your basic math operations

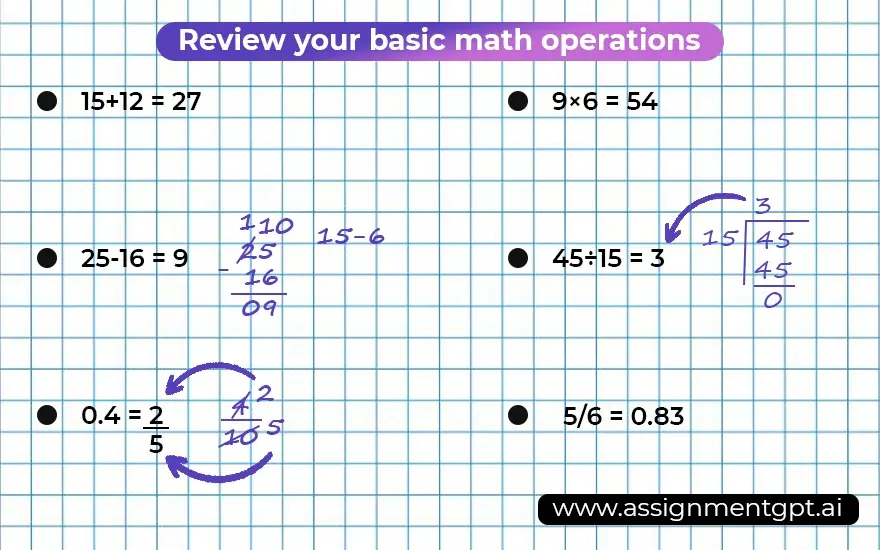
To begin learning basic algebra, you need to learn basic math skills like addition, subtraction, multiplication, and division.

[1] This basic/elementary school math is necessary before you start learning algebra.

[2] Without mastering these skills, it will be difficult to solve the more complex concepts taught in algebra. If you need additional information on these activities, try our article on basic math skills.

You don’t have to be great at doing these basic exercises in your head and doing algebra problems. Many algebra courses can use calculators to save time when doing these simple tasks. However, you should at least know when and how to do these things without calculators.

Know the order operations

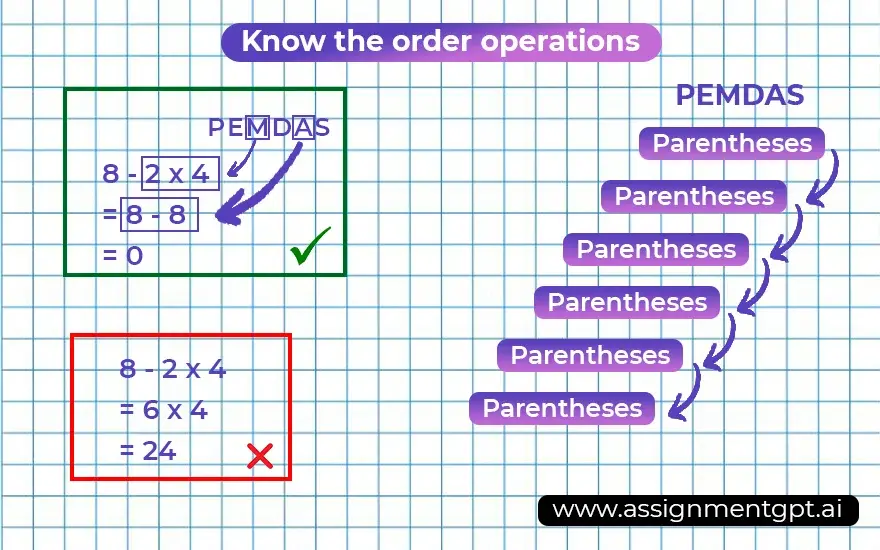
As a beginner, one of the most difficult tasks in solving an algebraic equation is knowing where to start. Fortunately, there is a common order for solving these problems: perform each mathematical operation in parentheses first, then perform the expression, then multiply, then divide, then add, and finally subtract in. A handy tool to remember this activity is the acronym PEMDAS ]. Learn how to use the operation sequence here . To recap, the sequence of operations is:

• Parentheses
• Exponents
• Multiplication
• Division
• Addition
• Subtraction

The order of operations is important in algebra because performing the operation in the wrong order in an algebra problem can sometimes affect the answer. For example, when solving the arithmetic problem 8 + 2 × 5, adding 2 to 8 first gives 10 × 5 = 50, but multiplying 2 and 5 first gives 8 + 10 = 18 . Second the answer is correct.

Know how to use negative numbers

Using negative numbers in algebra is common, so it is wise to review how to add, subtract, multiply, and divide negative numbers before you start learning algebra. Below are just a few negative number basics to keep in mind — our comments on adding and subtracting negative numbers Let’s take a look

• In the number path, the negative part of the number is equally distant from zero as the positive part, but in the opposite direction.
• Adding two negative numbers makes the number more negative (in other words, the numbers will be larger, but the number will be counted as smaller because it is negative).
• Two negative signs intersect - the subtraction of a negative number equals the addition of a positive number
• Positive answers are obtained by multiplying or dividing two negative numbers.
• Negative answers are obtained by multiplying or dividing a positive number by a negative number.

Know how to keep long problems organized

While basic algebra problems can be straightforward to solve, more complex problems take many, many steps. To avoid mistakes, organize your work by starting a new path with steps to solve each problem. When dealing with two-dimensional equations, try to write all equal signs ("="s) under each other.[5]This way, making mistakes somewhere will be easier great to find and fix . For example, to solve the equation 9/3 - 5 + 3 × 4, we can formulate our problem as follows:

9/3 - 5 + 3 × 4 9/3 - 5 + 12 3 - 5 + 12 3 + 7 10

2. Understanding Variables

Look for symbols that aren't numbers

In algebra, you begin to recognize letters and symbols that appear in your math problems, not just numbers. These are called variables. Changes are not as confusing as they might first appear - they are simply ways of representing a number of unfamiliar values. Below are a few common examples of algebraic transformations. Letters like x, y, z, a, b, and c Greek letters like theta, or θ Note that not all symbols are unknown variables. For instance, pi, or π, is always equal to about 3.14159.

Think of variables as unknown numbers

As noted above, fundamental changes are simply unknown values.[7] In other words, there is a number that can take the place of a variable to make the equation work. Usually, your goal in an algebra problem is to figure out what the variable is - think of it as a "mystery number" that you're trying to figure out. For example, in the equation 2x + 3 = 11, x is our variable. This means that a value is going to replace x so that the left side of the equation equals 11. Since 2 × 4 + 3 = 11, x = 4 in this case

An easy way to start understanding conversion is to substitute question marks in algebra problems. For example, we can repeat the equation 2 + 3 + x = 9 with 2 + 3 + ? = 9. This makes it easy to understand what we are trying to do - we just need to know how many to add to 2 + 3 = 5 to get 9. The answer again is 4, of course.

Watch for recurring variables

If a change appears more than once, simplify the changes. What do you do if the same variable appears more than once in the equation? While this situation may seem difficult to handle, you can actually handle variables as you would normal numbers — in other words, you can add, subtract, and so on until you can just sum the same variables In other words x + x = 2x , but x + y 2xy Not equal to this.

• For example, we consider the equation 2x + 1x = 9. In this case, we can combine 2x and 1x to get 3x = 9. Since 3 x 3 = 9, we know that x = 3 .
• Note again that you can add only similar changes. In the equation 2x + 1y = 9, we cannot add 2x and 1y because they are two different variables.
• This is also true when one variable has a different exponent than the other. For example, in the equation 2x + 3x2 = 10, we cannot combine 2x and 3x2 because the x variables have different exponents. See How to Add Exponents for more information.

Read this article also : Best Math Websites for Teachers and Students

3. Learning to solve Equations by Canceling

Try to get variable by itself in algebra equations

In algebra, solving an equation usually means figuring out what the variable is. Algebraic equations are often formulated on both sides with numerals and/or transformations, for example: x + 2 = 9 × 4. To find out what the transformation is, you need to get yourself on one side of the equal sign Whatever else on the other side of the equal sign is your answer.

• In the example (x + 2 = 9 × 4), we need to eliminate the "+ 2" to get x on its own on the left side of the equation. To do this, we simply subtract 2 from that side, leaving us with x = 9 × 4. However, to make both sides of the equation equal, we also need to subtract 2 from the other side This gives x = 9 × 4 - 2. Following the operations, multiply first, then, x = 36 - 2 = 34 we get the answer.

Cancel addition with subtraction (and vice versa)

As we saw just above, having x on one side of the equals sign by itself usually means eliminating the side digits. To do this, we perform the "opposite" operation on both sides of the equation. For example, in the equation x + 3 = 0, because we see "+ 3" next to our x, we put "- 3" on both sides. "+ 3" and "- 3", leaving x itself as "-3" on the other side of the equal sign, if x = -3.

• Often, it's like adding and subtracting "opposites" - do one and eliminate the other. See below: For addition, subtract. Example: x + 9 = 3 → x = 3 - 9 For subtraction, add. Example: x - 4 = 20 → x = 20 + 4

Cancel multiplication with division (and vice versa)

Multiplication and division are a bit harder to work with than addition and subtraction, but they have the same "inverse" relationship. If you see "× 3" on one side, dividing both sides by 3 will cancel and so on.

• If you use multiplication and division, you must do the opposite operation on anything on the other side of the even sign, even if it is more than one digit. See below:

For multiplication, divide. Example: 6x = 14 + 2→ x = (14 + 2)/6 For division, multiply. Example: x/5 = 25 → x = 25 × 5

Cancel exponents by taking the root (and vice versa)

The exponents pre-algebra topic is pretty advanced — if you don’t know how, check out our basic exponent chart for more information. The "opposite of the killer" has the same number as the root. For example, the opposite of the 2 exponent is the square root (√), the opposite of the 3 exponent is the cube root (3√), and so on.[8]

• It may be a bit confusing, but, in these cases, you root for both sides when dealing with the coach. In other words, you take the references of both sides when dealing with the root. See below: For exponents, take the root. Example: x2 = 49 → x = √49 For roots, take the exponent. Example: √x = 12 → x = 122

4. Sharping your algebra skills

Use picture to make problems clearer

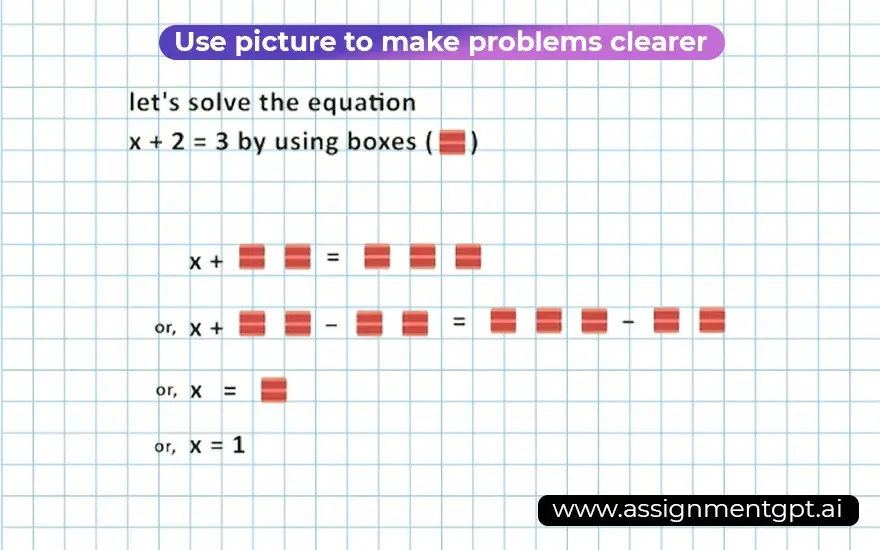If you have trouble visualizing an algebra problem, try using a picture or diagram to illustrate your equation. If you have something handy, you can also try using bunches of physical objects (such as blocks or coins) instead.

• For example, let's solve the equation x + 2 = 3 by using boxes (☐)

x +2 = 3

☒+☐☐ =☐☐☐

At this point, we'll subtract 2 from both sides by simply removing 2 boxes (☐☐) from both sides:

☒+☐☐-☐☐ =☐☐☐-☐☐

☒=☐, or x = 1

• As another example, let's try 2x = 4

☒☒ =☐☐☐☐

At this point, we'll divide both sides by two by separate the boxes on each side into two groups:

☒|☒ =☐☐|☐☐

☒ = ☐☐, or x = 2

Use common sense checks(especially for word problems)

When converting a word problem to algebra, try testing your formula by entering simple values for your variables. Does your equation make sense when x=0? When x=1? When x = -1? It’s easy to make simple mistakes by typing p=6d when you mean p=d/6, but it’s easy to catch these if you do a quick review of your work before continuing

• For example, suppose we are told that the football field is 30 feet (27.4 meters) longer than it is wide. We use the equation l = w + 30 to represent this. We can test whether this equation makes sense by plugging in simple values for w. For example, if the width of the area w = 10 feet (9.1 m), it becomes 10 feet + 30 = 40 feet (36.6 m). If the width is 30 ft (27.4 m), the length will be 30 ft + 30 = 60 ft (54.9 m), and so on. This makes sense — the wider the field, the longer we expect it to last, so this equation makes sense.

Be aware that answer won't always be integers in algebra

In algebra and other forms of advanced mathematics, the answer is not always a round and simple number. It can usually be decimals, fractions, or irrational numbers. Mathematics can help you find these difficult answers, but keep in mind that your teacher may ask that you give the answer in its exact form, not in inconvenient decimals

• For example, let’s say we round up a basic algebra equation to x = 12507. Typing 12507 into a calculator gives us a huge string of decimals (plus, just because the calculator screen is so big, it can’t show all the answers . ) In this case we 12507 only want to represent our answer, otherwise we want to simplify the answer by writing scientific notation.

Try expanding your skill

If you feel confident in basic algebra, give it a try. All algebraic knowledge has one of the most complex features — a simple way to get complex equations into a simple form. Factoring is a semi-advanced algebra topic, so if you’re having trouble mastering it, consider checking out the article linked above. Below are a few quick tips for multiplying equations.

• Equations with the form ax + ba factor to a(x + b). Example: 2x + 4 = 2(x + 2)
• Equations with the form ax2 + bx factor to cx((a/c)x + (b/c)) where c is the biggest number that divides into a and b evenly. - - --- Example: 3y2 + 12y = 3y(y + 4)
• Equations with the form x2 + bx + c factor to (x + y)(x + z) where y × z = c and yx + zx = bx. Example: x2 + 4x + 3 = (x + 3)(x + 1).

Ready to tackle algebra with confidence?
Start by reviewing your primary math skills and learning how to solve basic algebra equations. If you need additional help, seek assistance from your teacher or educational resources like Assignmentgpt AI.

Practice, Practice, Practice,

Algebra (and any other math) requires a lot of effort and repetition to improve. Don’t worry - by listening to your thoughts in class, being able to do all the work, and seeking help from your teacher or other students when needed, algebra will start to become second nature Ask your teacher to help you understand tricky algebra topics

Try Assignmentgpt AI for your all algebra question

AssignmentGPT AI solves algebra questions for students through a variety of features that simplify the process. It provides homework solutions, assignment writing, mathematical problem solving, image generation, and instant code solutions. In addition, AssignmentGPT AI aims to streamline the learning experience by generating homework assignments, making it less demanding and more useful for students. This AI tool is designed to complement traditional teaching methods by enhancing understanding, skill development and knowledge application, ultimately transforming the learning journey for students.

Conclusion

Algebra can also appear daunting at the start, but by using breaking it down into potential steps and practising frequently, you may conquer any demanding situations. Remember to build a sturdy basis in primary math abilities, grasp the idea of variables, and broaden hassle-fixing strategies. Don't hesitate to invite for assist whilst needed, and preserve working towards until algebra will become 2nd nature to you.

FAQs